Question

Find all values of x that satisfy the equation below. (x + 1)² - 25/9
= 0​

Answer 1

Explanation:

Hey there!

Given equation is:

(x+1)² - 25/9 = 0

Then;

(x+1)² - (5/3)² = 0 ( since 5² = 25 and 3² = 9)

or, {(x+1)+5/3} { (x+1)-5/3} = 0. { use a² - b² = (a+b)(a-b) formula}

`( (3x + 3 + 5)/(3) )( (3x + 3 - 5)/(3) ) = 0`

`( (3x + 8)/(3) )( (3x - 2)/(3)) = 0`

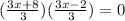
Now;

Either;

( \frac{3x + 8}{3}= 0

or, X = 8/3

Or,

( \frac{3x -2}{3} = 0

x = 2/3

Therefore, X = 8/3 or 2/3.

Hope it helps!

Answer 2

x = 8/3, 2/3

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Multiple Roots

Explanation:

Step 1: Define

Identify

(x + 1)² - 25/9 = 0

Step 2: Solve for x

1. [Addition Property of Equality] Add 25/9 on both sides: (x + 1)² = 25/9
2. [Equality Property] Square root both sides: x + 1 = ±5/3
3. [Subtraction Property] Subtract 1 on both sides: x = ±5/3 - 1
4. Evaluate Addition/Subtraction: x = 8/3, 2/3