Question

Can someone work please so I can understand how

Answer 1

Answer: Choice A)
`(4√(14))/(7)`

======================================================

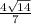
Step-by-step explanation:

Refer to the figure below. We start off drawing a right triangle that has opposite side sqrt(7) and adjacent side 5.

This is because tan = opposite/adjacent.

Use the pythagorean theorem to find the hypotenuse is sqrt(32) which simplifies like so

sqrt(32) = sqrt(16*2) = sqrt(16)*sqrt(2) = 4*sqrt(2)

The last thing to do is to take the ratio of the hypotenuse over the opposite side. Recall that csc, aka cosecant, is the reciprocal of sine.

sin = opposite/hypotenuse

csc = hypotenuse/opposite

---------

So we get the following

`\csc{\theta} = \frac{\text{hypotenuse}}{\text{opposite}}\\\\\csc{\theta} = (4√(2))/(√(7))\\\\\csc{\theta} = (4√(2)*√(7))/(√(7)*√(7))\\\\\csc{\theta} = (4√(2*7))/(√(7*7))\\\\\csc{\theta} = (4√(14))/(√(49))\\\\\csc{\theta} = (4√(14))/(7)\\\\`

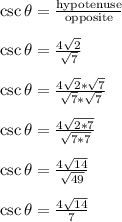
So that's why the answer is choice A.

Answer 2

`\text{A. }\frac{4√(14)}{{7}}`

Step-by-step explanation:

In any right triangle, the tangent of an angle is equal to its opposite side divided by its adjacent side. Therefore, we can form a right triangle with non-right angle
`\theta` and its opposite side
`√(7)` and its adjacent side
`5`.

By definition,
`\csc \theta=(1)/(\sin\theta)`.

In any right triangle, the sine of an angle is equal to its opposite side divided by the hypotenuse, or longest side, of the triangle. To find the hypotenuse, use the Pythagorean Theorem:
`a^2+b^2=c^2`, where
`c` is the hypotenuse, or longest side, of the right triangle and
`a` and
`b` are the two legs of the triangle.

Solving, we get:

`5^2+√(7)^2=c^2,\\25+7=c^2,\\c^2=32,\\c=√(32)=4√(2)`

Therefore, we have:

`\csc \theta = (1)/(\sin \theta)=(1)/((√(7))/(4√(2))),\\\\\csc \theta=1\cdot (4√(2))/(√(7)),\\\\\csc \theta =(4√(2))/(√(7))\cdot (√(7))/(√(7))=\boxed{\text{A. }\frac{4√(14)}{{7}}}`