Given:
Cards labelled 1, 3, 5, 6, 8 and 9.
A card is drawn and not replaced. Then a second card is drawn at random.
To find:
The probability of drawing 2 even numbers.
Solution:
We have,
Even number cards = 6, 8
Odd numbers cards = 1, 3, 5, 9
Total cards = 1, 3, 5, 6, 8 and 9
Number of even cards = 2
Number of total cards = 6
So, the probability of getting an even card in first draw is:
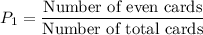
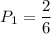

Now,
Number of remaining even cards = 1
Number of remaining cards = 5
So, the probability of getting an even card in second draw is:
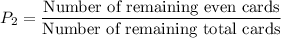
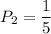
The probability of drawing 2 even numbers is:
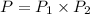
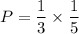
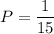
Therefore, the probability of drawing 2 even numbers is
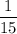 . Hence, the correct option is (b).
. Hence, the correct option is (b).