Answer:
This can be done in 3,060 ways.
Explanation:
Letters are chosen without replacement, and the order does not matter, which means that the combinations formula is used.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

In this question:
Four letters from a set of 18. So
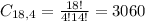
This can be done in 3,060 ways.