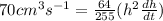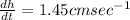Answer:
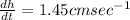
Explanation:
Rate of Water Fill
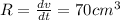
Length
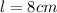
Height
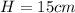
Water level
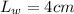
Generally the equation for relationship b/w h and a is mathematically given by
Since by the properties of similar triangles

Let
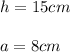
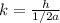
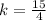
Therefore
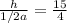
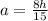
Generally the equation for volume of Pyramid is mathematically given by

Subsitute a
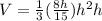
Therefore
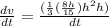
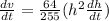
Since
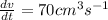
Therefore