Question

Suppose the demand function​ (D) for golf clubs​ is: Q​P, where P is the price paid by consumers in dollars per club and Q is the quantity demanded in thousands. Suppose the supply curve​ (S) for golf clubs is estimated to​ be: QP. Calculate the equilibrium price for golf clubs and the equilibrium quantity sold. The equilibrium price is ​$ 75 per club ​(Enter your response as an​ integer.)​, and the equilibrium quantity is 75 thousand clubs ​(Enter your response as an integer.​) Suppose instead that golf club producers agree to charge a price of ​$ per club. This would result in a surplus of nothing thousand clubs ​(Enter your response as an integer.​)

Answer 1

(a)

The equilibrium price is $75 per club

The equilibrium quantity is 75000 clubs

(b)

A charge a price of $​50 per club. This would result in a surplus of 25000 clubs

Step-by-step explanation:

Given

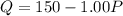`Q = 150 - 1.00P` --- The demand function

`Q = 1.00P` --- The supply function

Solving (a): The equilibrium price and quantity

To do this, we equate both functions

This gives:

`1.00P = 150 - 1.00P`

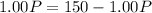
Collect like terms

`1.00P+1.00P = 150`

`2.00P = 150`

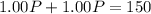
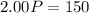
Make P the subject

`P =(150)/(2.00)`

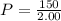
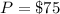`P = \$75` ---The equilibrium price

Substitute 75 for P in
`Q = 1.00P`

`Q = 1.00 * 75`

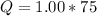
`Q = 75` ---- The equilibrium quantity

Solving (c): When the price is changed to $50

This means that:
`P =50`

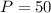
The quantity demanded will be:

`Q = 150 - 1.00P`

`Q = 150 - 1.00 * 50`

`Q = 150 - 50`

`Q = 100`

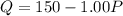
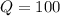
Subtract the equilibrium quantity from
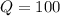`Q = 100` to get the shortage/surplus

`\triangle Q = 100 - 75`

`\triangle Q = 25`

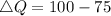
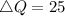
Since the change is positive, then there is a surplus.