Answer:
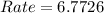
Explanation:
Given
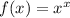 at
at
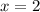
Required
The instantaneous rate of change
We have:
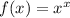
The instantaneous rate of change is:
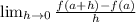
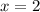 implies that:
implies that:
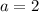
So, we have:
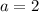
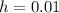
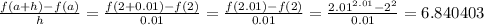
Keep reducing h but set a constant at 2
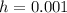
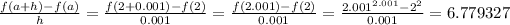
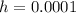
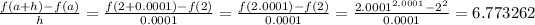
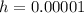
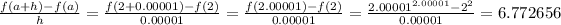
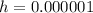
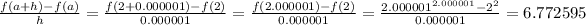
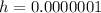
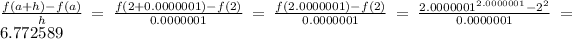
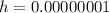
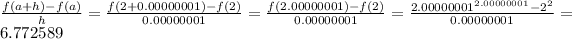
Notice that:
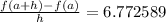 for
for
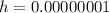 and
and
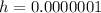
Hence, the instantaneous rate of change is:
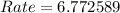
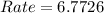 ---- approximated
---- approximated