Question

In a Gallup poll, 1025 randomly selected adults were surveyed and 29% of them said that they used the Internet for shopping at least a few times a year. Find a 99% confidence interval estimate of the proportion of adults who use the Internet for shopping.

Answer 1

Answer: (0.25,0.33)

Explanation:

A 99% confidence interval for population proportion is given by:-

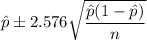`\hat{p}\pm 2.576\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`, where
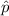`\hat{p}` = sample proportion,
`n` = sample size.

Given:
`n=1025, \hat{p}=0.29`

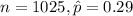
A 99% confidence interval estimate of the proportion of adults who use the Internet for shopping:

`0.29\pm 2.576\sqrt{(0.29(1-0.29))/(1025)}\\\\=0.29\pm 2.576√(0.00020087804878)\\\\=0.29\pm2.576(0.01417)\\\\=0.29\pm0.03650192\\\\=(0.29-0.03650192,\ 0.29+0.03650192)\\\\=(0.25349808,\ 0.32650192)`

`\approx(0.25,\ 0.33)`

Thus, a 99% confidence interval estimate of the proportion of adults who use the Internet for shopping = (0.25,0.33)