Question

PLEASE HELP ASAP: TRIGONOMETRY

Answer 1

Recall that sine is the ratio of opposite over hypotenuse, so we say

sin(theta) = opposite/hypotenuse

If we have a triangle labeled as such in the diagram below, then we can use symbols to write sin(theta) = A/C

Similarly, cos(theta) = B/C since cosine is the ratio of adjacent over hypotenuse.

Then from here we use a bit of algebra to compute the left hand side of the given equation. The goal is to see if we can simplify it to 1.

`\sin^2\left(\theta\right)+\cos^2\left(\theta\right)\\\\\left(\sin\left(\theta\right)\right)^2+\left(\cos\left(\theta\right)\right)^2\\\\\left((A)/(C)\right)^2+\left((B)/(C)\right)^2\\\\(A^2)/(C^2)+(B^2)/(C^2)\\\\(A^2+B^2)/(C^2)\\\\(C^2)/(C^2)\\\\1`

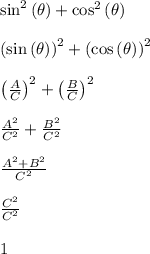
So this shows that the left hand side is identically the same as the right hand side (both sides are 1), and it doesn't matter what you replace theta with. Theta can be any real number and the equation will always be true.

Note: if you're wondering how A^2+B^2 became C^2, it's because of the pythagorean theorem. So that's why this trig identity is often referred to as the pythagorean trig identity.