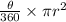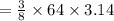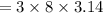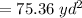Question

Find the indicated area of the sector surrounded in bold.

Answer 1

75.36 yd² (≈ 75.4 yd²)

Explanation:

GIVEN :-

• Angle subtended by the arc at center of circle (θ) = 135°
• Radius of the circle = 8 yd

TO FIND :-

• Area of the sector

GENERAL FORMULAE TO BE USED IN THI QUESTION :-

Lets say there's an arc which subtends θ angle in the center of the circle & radius of the circle is 'r'.

Area of the sector =
`(\theta)/(360) * \pi r^2`

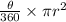
SOLUTION :-

Area of the sector =
`(\theta)/(360) * \pi r^2`

`= (135)/(360) * \pi (8)^2`

`= (3)/(8) * 64 * 3.14`

`= 3 * 8 * 3.14`

`=75.36 \; yd^2`