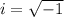Problem 1
Answer: The roots are x = 0, x = 2, x = -3
------------------
Step-by-step explanation:
The term "root" is another way of saying "zeros of a function" or "x intercept".
To find the roots, set each factor equal to zero and solve for x.
x-2 = 0 solves to x = 2, while x+3 = 0 solves to x = -3
========================================================
Problem 2
Answer: Roots are x = 1,
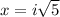 and
and

------------------
Step-by-step explanation:
Factor by grouping
x^3 - x^2 + 5x - 5 = 0
(x^3 - x^2) + (5x - 5) = 0
x^2(x - 1) + 5(x - 1) = 0
(x^2 + 5)(x - 1) = 0
x^2 + 5 = 0 solves to the roots
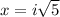 and
and

x-1 = 0 solves to x = 1
Note: