Question

Box A has 14 black pens and 6 blue pens box B has 9 black pens and 3 blue pens a pen is randomly chosen from each box list these events from least likely to most likely

Answer 1

The list of these events from least likely to most likely is Blue-Blue -> Black-Blue -> Blue-Black -> Black-Black

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

Possible outcomes:

Black - Black

Black - Blue

Blue - Black

Blue - Blue

Probability of each outcome:

Black-Black:

14 out of 20, and then 9 out of 12. So

`P_(BkBk) = (14)/(20) * {9}{12} = (14*9)/(20*12) = (126)/(240)`

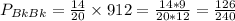
Black-Blue:

14 out of 20, then 3 out of 12. So

`P_(BkBl) = (14)/(20) * {3}{12} = (14*3)/(20*12) = (42)/(240)`

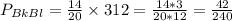
Less likely than black-black.

Blue - Black:

6 out of 20, then 9 out of 12. SO

`P_(BlBk) = (6)/(20) * {9}{12} = (6*9)/(20*12) = (54)/(240)`

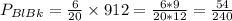
More likely than black-blue, less likely than black-black.

Blue - Blue

6 out of 20, then 3 out of 12

`P_(BlBl) = (6)/(20) * {3}{12} = (6*3)/(20*12) = (18)/(240)`

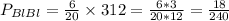
Least likely of the outcomes.

List these events from least likely to most likely:

The list of these events from least likely to most likely is Blue-Blue -> Black-Blue -> Blue-Black -> Black-Black