Answer:
The surveyor is 36.076 kilometers far from her camp and her bearing is 16.840° (standard form).
Explanation:
The final position of the surveyor is represented by the following vectorial sum:
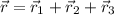 (1)
(1)
And this formula is expanded by definition of vectors in rectangular and polar form:
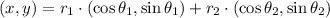 (1b)
(1b)
Where:
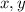 - Resulting coordinates of the final position of the surveyor with respect to origin, in kilometers.
- Resulting coordinates of the final position of the surveyor with respect to origin, in kilometers.
 - Length of each vector, in kilometers.
- Length of each vector, in kilometers.
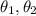 - Bearing of each vector in standard position, in sexagesimal degrees.
- Bearing of each vector in standard position, in sexagesimal degrees.
If we know that
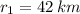 ,
,
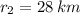 ,
,
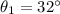 and
and
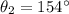 , then the resulting coordinates of the final position of the surveyor is:
, then the resulting coordinates of the final position of the surveyor is:
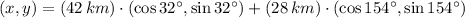
![(x,y) = (35.618, 22.257) + (-25.166, 12.274)\,[km]](https://img.qammunity.org/2022/formulas/mathematics/high-school/zvx9hok8gxsxl541ll0dloxhs2eod3vmsw.png)
![(x,y) = (10.452, 34.531)\,[km]](https://img.qammunity.org/2022/formulas/mathematics/high-school/zx2eocuqian8yk7nmmnds80ec4qpuncmrg.png)
According to this, the resulting vector is locating in the first quadrant. The bearing of the vector is determined by the following definition:
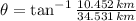

And the distance from the camp is calculated by the Pythagorean Theorem:

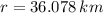
The surveyor is 36.076 kilometers far from her camp and her bearing is 16.840° (standard form).