Answer:
- The graph is shown below
- Vertex = (2,1)
- Axis of symmetry is x = 2
- Domain = set of all real numbers
- Range = set of y values such that
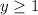
=======================================================
Step-by-step explanation:
Use your favorite graphing tool to graph the equation. If your teacher doesn't allow you to use graphing software, then you'll have to plug in various x values to find the paired y values. This gives the set of (x,y) points needed to be plotted to form the parabola. The more points you plot, the more accurate the curve.
The graph is shown below. I used GeoGebra to make the graph. It's free graphing software. Desmos is another tool that I recommend.
------------
The lowest point on the parabola is the vertex (h,k) = (2,1) which is shown in the graph below.
This is due to the equation being in vertex form y = a(x-h)^2 + k. We see that h = 2 and k = 1.
-------------
The axis of symmetry is the vertical line that passes through the vertex.
As such, the axis of symmetry equation is simply x = h. So that's how we get to x = 2.
In the graph below, the axis of symmetry is the red dashed line.
-------------
There aren't any restrictions on x. We don't have to worry about dividing by zero or applying a square root to a negative number.
Therefore, any x value is allowed and the domain is the set of all real numbers.
-------------
The range however isn't the set of all real numbers. The lowest y can get is y = 1 due to the vertex point. We can have y = 1 or larger
Therefore,
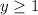 is the range.
is the range.