Question

The reaction of iron (III) oxide with carbon monoxide produces iron and carbon dioxide.

Fe,O3(s) + 3CO(g) - 2Fe(s) + 3C0 (9)
If you have 39.5g of Fe2O3, how many grams of CO are required for a complete reaction?

Answer 1

21g

Step-by-step explanation:

no.ofmol fe2o3=39.5/(56×2+16×3)=0.25mol

from equation 1mole fe2o3 react with 3mole co

so,0.25mol fe2o3 react with 0.75mol co

mass of co=0.75×(12+16)=21g

Answer 2

Approximately
`20.8\; \rm g`.

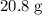Step-by-step explanation:

`\rm Fe_2O_3 \, (s) + 3\; CO\, (g) \to 2\; Fe\, (s) + 3\; CO_2\, (g)`.

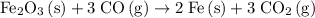Relative atomic mass:

• 
  `\rm Fe`:
  `55.845`.
• 
  `\rm C`:
  `12.011`.
• 
  `\rm O`:
  `15.999`.

Formula mass:

`\begin{aligned}M({\rm Fe_2O_3}) &= 2 * 55.845 + 3 * 15.999\\ &= 159.687\; \rm g \cdot mol^(-1)\end{aligned}`.

`\begin{aligned}M({\rm CO}) &= 12.011 + 15.999\\ &= 28.010\; \rm g \cdot mol^(-1)\end{aligned}`.

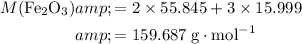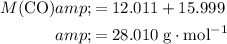Number of moles of
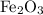`\rm Fe_2O_3` formula units in
`39.5\; \rm g` of this compound:

`\begin{aligned}&n({\rm Fe_2O_3}) \\ &= \frac{m({\rm Fe_2O_3})}{M({\rm Fe_2O_3})} \\ &= (39.5\; \rm g)/(159.687\; \rm g \cdot mol^(-1))\approx 0.247\; \rm mol\end{aligned}`.

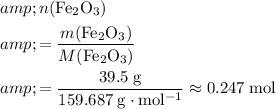Refer to the balanced equation for this reaction.

• Coefficient of
  `\rm Fe_2O_3`:
  `1`.
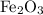• Coefficient of
  `\rm CO`:
  `3`.

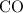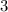Hence, for every formula unit of
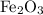`\rm Fe_2O_3` that this reaction consumes,
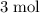`3\; \rm mol` of
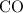`\rm CO` molecules would also need to be consumed. Therefore, if neither reactant is in excess:

`\displaystyle \frac{n({\rm CO})}{n({\rm Fe_2O_3})} = (3)/(1) = 3`.

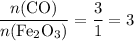Calculate the number of moles of
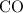`\rm CO` required to react with that
`39.5\; \rm g` of
`\rm Fe_2O_3`:

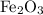`\begin{aligned}&n({\rm CO}) \\ &= n({\rm Fe_2O_3}) \cdot \frac{n({\rm CO})}{n({\rm Fe_2O_3})} \\[0.5em] &\approx 0.247\; \rm mol * 3 \approx 0.742\; \rm mol\end{aligned}`.

Make use of the formula mass of
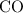`\!\rm CO` to find the mass of that
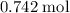`0.742\; \rm mol` of
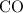`\rm CO` molecules:

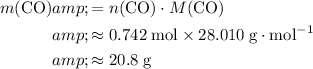`\begin{aligned} m({\rm CO}) &= n({\rm CO}) \cdot M({\rm CO}) \\ &\approx 0.742\; \rm mol * 28.010\; \rm g \cdot mol^(-1) \\ &\approx 20.8\; \rm g\end{aligned}`.