Answer:
The horizontal component of the vector is approximately -16.07
The vertical component of the vector is approximately 19.15
Step-by-step explanation:
A vector quantity is a quantity that posses both magnitude and direction specifications
The magnitude of the given vector, R = 25 units
The direction of the vector, θ = 130°
Therefore the location of the vector, starting from the origin of the Cartesian plane, is in the second quadrant having an angle of 180° - 130° = 50° to the horizontal
Given that the x-coordinate is negative in the second quadrant, we have;
The horizontal component of the vector, Rₓ = The x-coordinate of the vector = R×cos(θ)
∴ The horizontal component of the vector, Rₓ = 25 × cos(130°) = -25 × cos(50°) ≈ -16.07
The horizontal component of the vector, Rₓ ≈ -16.07
The vertical component of the vector,
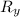 = The y-coordinate of the vector = R×sin(θ)
= The y-coordinate of the vector = R×sin(θ)
∴ The vertical component of the vector,
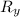 = 25 × sin(130°) ≈ 19.15
= 25 × sin(130°) ≈ 19.15
The vertical component of the vector,
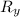 ≈ 19.15
≈ 19.15
The vector can be resolved as R = -16.07·i + 19.15·j