Question

In a sample of 230 teenagers, 202 would like to have smaller class sizes at their school. Find the sample

proportion, the margin of error, and the interval likely to contain the true population proportion. If
necessary, round your answers to the nearest percent.

Answer 1

The sample proportion is 0.88.

The margin of error is of 0.04.

The interval likely to contain the true population proportion is (0.84,0.92).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

Margin of error:

The margin of error is of:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

Sample of 230 teenagers, 202 would like to have smaller class sizes at their school.

This means that
`n = 230`, and that the sample proportion is:

`\pi = (202)/(230) = 0.88`

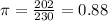
The sample proportion is 0.88.

Standard 95% confidence level

So
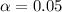`\alpha = 0.05`, z is the value of Z that has a p-value of
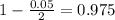`1 - (0.05)/(2) = 0.975`, so
`Z = 1.96`.

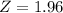Margin of error:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`M = 1.96\sqrt{(0.88*0.12)/(230)}`

`M = 0.04`

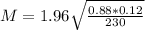
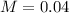
The margin of error is of 0.04.

Confidence interval:

Sample proportion plus/minus margin of error. So

0.88 - 0.04 = 0.84

0.88 + 0.04 = 0.92

The interval likely to contain the true population proportion is (0.84,0.92).