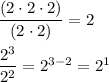Question

2^5×8^4/16=2^5×(2^a)4/2^4=2^5×2^b/2^4=2^c
A=
B=
C=
Please I'm gonna fail math

Answer 1

9514 1404 393

Answer:

a = 3, b = 12, c = 13

Explanation:

The applicable rules of exponents are ...

(a^b)(a^c) = a^(b+c)

(a^b)/(a^c) = a^(b-c)

(a^b)^c = a^(bc)

___

You seem to have ...

`(2^5*8^4)/(16)=(2^5*(2^3)^4)/(2^4)\qquad (a=3)\\\\=(2^5*2^(3\cdot4))/(2^4)=(2^5*2^(12))/(2^4)\qquad (b=12)\\\\=2^(5+12-4)=2^(13)\qquad(c=13)`

_____

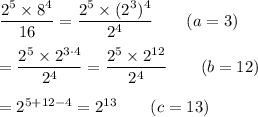
Additional comment

I find it easy to remember the rules of exponents by remembering that an exponent signifies repeated multiplication. It tells you how many times the base is a factor in the product.

`2\cdot2\cdot2 = 2^3\qquad\text{2 is a factor 3 times}`

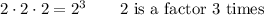
Multiplication increases the number of times the base is a factor.

`(2\cdot2\cdot2)*(2\cdot2)=(2\cdot2\cdot2\cdot2\cdot2)\\\\2^3*2^2=2^(3+2)=2^5`

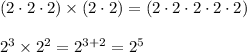
Similarly, division cancels factors from numerator and denominator, so decreases the number of times the base is a factor.

`((2\cdot2\cdot2))/((2\cdot2))=2\\\\(2^3)/(2^2)=2^(3-2)=2^1`