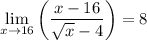Question

`\lim_(h \to \116) x-16/√(x) -4`
What is the limit?

Answer 1

`\displaystyle 8`

Explanation:

we would like to compute the following limit

`\displaystyle \lim_(x \to 16) \left( (x - 16)/( √(x) - 4) \right)`

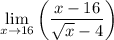
if we substitute 16 directly we'd end up

`\displaystyle = (16 - 16)/( √(16) - 4)`

`\displaystyle = (0)/( 0)`

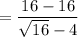
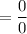
which isn't a good answer now notice that we have a square root on the denominator so we can rationalise the denominator to do so multiply the expression by √x+4/√x+4 which yields:

`\displaystyle \lim_(x \to 16) \left( (x - 16)/( √(x) - 4) * ( √(x) + 4 )/( √(x) + 4 ) \right)`

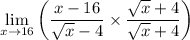
simplify which yields:

`\displaystyle \lim_(x \to 16) \left( ((x - 16)( √(x) + 4))/( x - 16) \right)`

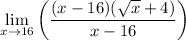
we can reduce fraction so that yields:

`\displaystyle \lim_(x \to 16) \left( \frac{ \cancel{(x - 16)}( √(x) + 4)}{ \cancel{x - 16} } \right)`

`\displaystyle \lim _(x \to 16) \left( √(x ) + 4\right)`

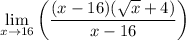
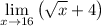
now it's safe enough to substitute 16 thus

substitute:

`\displaystyle = √(16) + 4`

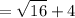
simplify square root:

`\displaystyle = 4 + 4`

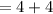
simplify addition:

`\displaystyle = 8`

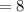
hence,

`\displaystyle \lim_(x \to 16) \left( (x - 16)/( √(x) - 4) \right) = 8`