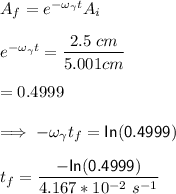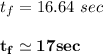Question

A vertical spring with a spring constant of 2.00 N/m has a 0.30-kg mass attached to it, and the mass moves in a medium with a damping constant of 0.025 kg/s. The mass is released from rest at a position 5.0 cm from the equilibrium position. How long will it take for the amplitude to decrease to 2.5 m?

Answer 1

17 seconds

Step-by-step explanation:

Given that:

The mass attached to the spring (m) = 0.30 kg

The spring constant (k) = 2.00 N/m

The damping constant (b) = 0.025 kg/s

The initial distance
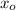`x_o` = 5.0 cm

The initial final amplitude
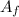`A_f` = 2.5 cm and not 2.5 m, please note the mistake, if it is 2.5 m, our time taken will be -93.7 sec, and we do not want a negative time value.

To start with the angular frequency damping using the formula:

`\omega_(\gamma)= (b)/(2m)`

`\omega_(\gamma)= (0.025 \ kg/s)/(2(0.3 \ kg))`

`\omega_(\gamma)=4.167 * 10^(-2) \ s^(-1)`

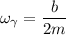
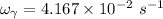
In the absence of damping, the angular frequency is:

`\omega_o = \sqrt{(k)/(m)}`

`\omega_o = \sqrt{(2 \ N/m)/(0.3 kg)} \\\\\omega_o = 2.581 \ s^(-1)`

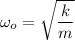
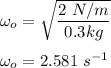
The initial amplitude oscillation can be computed by using the formula:

`A_i = e^{-\omega_(\gamma)t} x_o \sqrt{(\omega_o^2)/(\omega_o^2-\omega_f^2)}`

`A_i = e^{-\omega_(\gamma)0} (5.0 \ cm) \sqrt{(2.581^2)/(2.581^2-(4.167*10^(-2))^2)}`

`A_i = 5.0006 \ cm \\ \\ A_i = 5.001 \ cm`

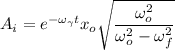
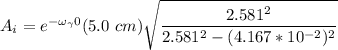
The final amplitude, as well as the initial amplitude, can be illustrated by using the relation:

`A_f = e^{-\omega_(\gamma)t}A_i\\ \\ e^{-\omega_(\gamma)t} = (2. 5 \ cm)/(5.001 cm)\\ \\ = 0.4999\\ \\ \implies -\omega_(\gamma)t_f = \mathsf{In (0.4999)} \\ \\ t_f = \frac{\mathsf{-In (0.4999)}}{4.167*10^(-2) \ s^(-1)} \\ \\`

`t_f = 16.64 \ sec \\ \\ \mathbf{t_f \simeq 17 sec}`