Answer:
Explanation:
The first one gives us everything we need except the radius, which is easy enough to solve for if you're careful with your algebra. The area of a sector of a circle is given as:
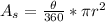 where θ is the measure of the central angle of the circle. For us, that fills in as follows:
where θ is the measure of the central angle of the circle. For us, that fills in as follows:
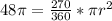 and manipulate it as follows:
and manipulate it as follows:
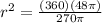 the π's cancel out, leaving us with simple multiplication and division to get
the π's cancel out, leaving us with simple multiplication and division to get
r = 8. Now for the next one, which is a bit more involved.
In order to find the area of the shaded part, we need to find the area of the right triangle there and subtract it from the area of the sector of the circle. First the area of the sector, which is given as:
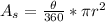 where θ again is the measure of the central angle of the circle, 90°:
where θ again is the measure of the central angle of the circle, 90°:
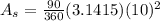 which simplifies a bit to
which simplifies a bit to
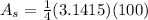 , giving us an area of
, giving us an area of
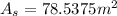 . Now onto the area of the triangle.
. Now onto the area of the triangle.
Since this triangle is inscribed in the circle and the circle's radius is 10, tha also gives us both the height and the base measures of the triangle. The area then is:
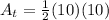 which is
which is
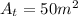
Subtract that from the area of the sector to get that the shaded area is 28.5 square meters, choice A.