Question

1. since A^2= 36x^2, a=?
2. since b^2= 49, b=?

Answer 1

D

Explanation:

36x² - 49 ← is a difference of squares and factors in general as

a² - b² = (a - b)(a + b)

then

36x² - 49

= (6x)² - 7²

= (6x - 7)(6x + 7)

Thus 6x - 7 is a factor of the expression

Answer 2

We need to simplify the expression 36x² - 49 , but let's recall the identity which is the main key to solve this question i.e

• 
  `{\boxed{\bf{a^(2)-b^(2)=(a+b)(a-b)}}}`

So , here we can write the above expression as

`{:\implies \quad \sf (6x)^(2)-(7)^(2)}`

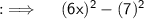
Now , using the above identity this can be written as :

`{:\implies \quad \sf (6x-7)(6x+7)}`

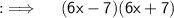
So , here both (6x-7) and (6x+7) are factors of 36x²- 49 , but in the options their is only 6x - 7.

Hence , Option D) 6x - 7 is correct

As here , 36x² = (6x)² = a² , so a = 6x and as 49² = 7² = b² , so b = 7