Answer:
(a) The force, acting on object 'C' is approximately 2.66972 × 10⁻¹⁰ Newtons
(b) The distance of 'C' from 'A', in the direction particle 'B' if there is no meters gravitational force acting on 'C' is appromimately 0.829 meters or 1.877 meters
Step-by-step explanation:
The given parameters are;
The mass of particle, A, m₁ = 2 kg
The mass of particle, B, m₂ = 0.3 kg
The mass of particle, C, m₃ = 0.05 kg
The distance between particle 'A' and particle 'B', r₁ = 0.15 m
The distance between particle 'B' and particle 'C', r₂ = 0.05 m
(a) The gravitational force, 'F', is given as follows;
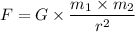
Where;
F = The force between the two masses
G = The gravitation constant = 6.67430 × 10⁻¹¹ N·m²/kg²
m₁ = The mass of object 1
m₂ = The mass of object 2
If 'C' is placed at 0.05 m from 'B', we have;
F₂₃ = 6.67430 × 10⁻¹¹ × 0.05 × 0.3/(0.05²) ≈ 4.00458 × 10⁻¹⁰
The gravitational force between force between particle 'B' and particle 'C', F₂₃ = 4.00458 × 10⁻¹⁰ N (towards the right)
F₁₃ = 6.67430 × 10⁻¹¹ × 0.05 × 2/(0.1²) ≈ × 10⁻¹⁰
The gravitational force between force between particle 'A' and particle 'B', F₁₃ = 6.6743 × 10⁻¹⁰ N (towards the left)
The force, 'F', acting on object 'C' = F₁₃ - F₂₃
F = (6.6743 - 4.00458) × 10⁻¹⁰ = 2.66972 × 10⁻¹⁰ N
The force, acting on object 'C' ≈ 2.66972 × 10⁻¹⁰ N
(b), When there is no gravitational force acting on 'C', let the distance of 'C' from 'A' = x
We have;
F₂₃ = F₁₂
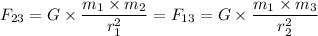
By plugging in the values and removing like terms, we get;
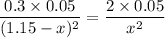
(1.15 - x)² × 2 × 0.05 = 0.3 × 0.05 × x²
0.1·x² - 0.23·x + 1.3225 = 0.015·x²
0.1·x² - 0.23·x + 1.3225 - 0.015·x² = 0
0.085·x² - 0.23·x + 0.13225= 0
x = (0.23± √((-0.23)² - 4 × 0.085 × ( 0.13225)))/(2 × 0.085))
x ≈ 0.829, or x ≈ 1.877
Therefore, the distance of 'C' from 'A', if there is no gravitational force acting on 'C', x ≈ 0.829 m, or x = 1.877 m, in the direction of 'B'