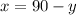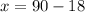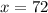Question

The Royal Fruit Company produces two types of fruit drinks. The first type is pure fruit juice, and the second type is pure fruit juice. The company is attempting to produce a fruit drink that contains pure fruit juice. How many pints of each of the two existing types of drink must be used to make pints of a mixture that is pure fruit juice

Answer 1

72 pints of the first type

18 pints of the second type

Explanation:

See attachment for complete question

Given

`x \to` first type

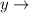`y \to` second type

Final volume = 90; So:

`x + y = 90`

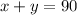
From the question, we understand that:

70% of x and 95% of y gives 75% of the fruit juice

This is represented as:

`70\% * x + 95\% * y = 75\%* 90`

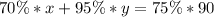
Make x the subject in
`x + y = 90`

`x = 90 - y`

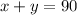
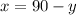
Substitute:
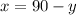`x = 90 - y` in
`70\% * x + 95\% * y = 75\% * 90`

`70\% * (90 - y) + 95\% * y = 75\% *90`

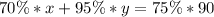
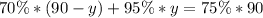
Express percentage as decimal

`0.70 * (90 - y) + 0.95 * y = 0.75 * 90`

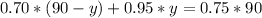
Open brackets

`63 - 0.70y + 0.95y = 67.5`

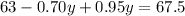
Collect like terms

`- 0.70y + 0.95y = 67.5 - 63`

`0.25y = 4.5`

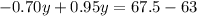
Divide both sides by 0.25

`y = (4.5)/(0.25)`

`y = 18`

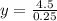
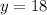
Recall that:
`x = 90 - y`

`x = 90 - 18`

`x = 72`