Solution :
From the Newton's second law of motion :
F = ma
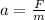
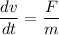
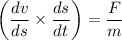

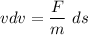
Integrating above the expression by applying the limits :
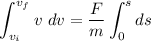
Here the diameter is s= D
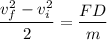
The final speed of the particle after travelling distance D is
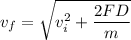
The kinetic energy of the particle of mass M is :

For M = 3M
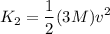

Thus the kinetic energy increases by a factor of 3.
The work done depends on the factor and the displacement of the body. Thus, the work done remains same even though the mass increases. Hence the work down increases by factor 1.