Answer:
a) 0.035 = 3.5% probability that a customer is a good risk and has filed a claim.
b) 0.0395 = 3.95% probability that the customer has filed a claim.
c) 0.8861 = 88.61% probability that the customer is a good risk
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
a) What is the probability that the customer is a good risk and has filed a claim?
70% are good risks.
Of those, 0.5% file a claim. So
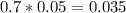
0.035 = 3.5% probability that a customer is a good risk and has filed a claim.
b) What is the probability that the customer has filed a claim?
0.5% of 70%(good risks)
1% of 20%(medium risks)
2.5% of 10%(poor risks). So
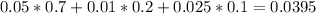
0.0395 = 3.95% probability that the customer has filed a claim.
c) Given that the customer has filed a claim, what is the probability that the customer is a good risk?
0.0395 = 3.95% probability that the customer has filed a claim means that
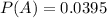
0.035 = 3.5% probability that a customer is a good risk and has filed a claim means that
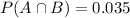
Thus
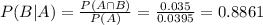
0.8861 = 88.61% probability that the customer is a good risk