Question

) As an ice cube melts its surface area is decreasing at a rate of 6cm2/sec. Find the rate at which the length of each side is decreasing at the moment when each side has length 2 cm. [Hint: a cube has 6 sides and each side has area x 2 where x is the side length]

Answer 1

The rate of decreasing of the length is 0.25 cm/s.

Explanation:

The surface area of the ice cube is:

`A_(ice)=6x^(2)`

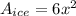
Where x is the side of the cube.

Let's take the derivative of A with respect to "t" to get the rate of change.

`(dA_(ice))/(dt)=12x(dx)/(dt)`

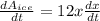
We know that dA/dt = 6 cm²/s and x is 2 cm, so we just need to solve it for dx/dt which is the rate change of the length.

`6=12(2)(dx)/(dt)`

`(dx)/(dt)=(1)/(4)\: cm/s`

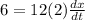
Therefore, the rate of decreasing of the length is 0.25 cm/s.

I hope it helps you!