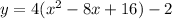Answer:
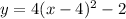
or

Explanation:
Given
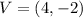 --- vertex
--- vertex
 --- point
--- point
Required
The equation of the parabola
The equation of the parabola is of the form
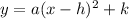
Where
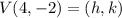 ---- the vertex
---- the vertex
So, we have:
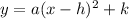
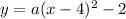
In
 , we have:
, we have:

Substitute
 in
in
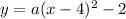
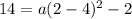
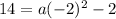
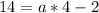
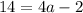
Collect like terms
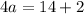
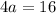
Divide both sides by 4
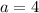
So:
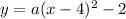 becomes
becomes
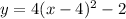
Open bracket to express the equation in standard form