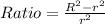Answer:
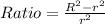
Explanation:
Given
See attachment for circles
Required
Ratio of the outer sector to inner sector
The area of a sector is:

For the inner circle
The sector of the inner circle has the following area
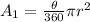
For the whole circle
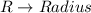
The sector of the outer sector has the following area
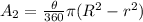
So, the ratio of the outer sector to the inner sector is:
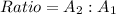

Cancel out common factor

Express as fraction