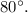Question

In circle O, PQ is a tangent and PRT is a secant. If angle P is 56 degrees and arc QT is 192 degrees, what is the measure of arc QR(type in numbers only)

Answer 1

80, I got it right so you should get it too

Answer 2

The measure of arc QR in the circle is
`\( 80^\circ \).`

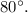
To find the measure of arc QR in circle O, given that PQ is a tangent and PRT is a secant, we can use the properties of circles and their angles:

1. The angle formed by a tangent and a secant is equal to half the difference of the measures of the intercepted arcs. In other words, the angle outside the circle angle P is equal to
`\( (1)/(2)(\text{arc} QT - \text{arc} QR) \)`.

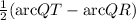2. We are given:

`- \( \angle P = 56^\circ \)`

-
`\( \text{arc} QT = 192^\circ \)`

3. The formula relating the angle and arcs is:

`\[ \angle P = (1)/(2)(\text{arc} QT - \text{arc} QR) \]`

4. Plugging in the known values, we get:

`\[ 56 = (1)/(2)(192 - \text{arc} QR) \]`

5. To solve for
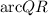`\( \text{arc} QR \)`, we multiply both sides by 2 and then add
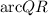`\( \text{arc} QR \)` to both sides:

`\[ 112 = 192 - \text{arc} QR \]`

`\[ \text{arc} QR = 192 - 112 \]`

6. Calculate the result to find
`\( \text{arc} QR \).`

arc QR =
`\( 80^\circ \).`