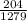Question

An amusement park has two featured rides that require an additional ticket, the Slingshot and the Scream Flyer. On a summer day, 1279 visitors entered the park. 280 visitors bought tickets for either the Slingshot or the Scream Flyer. 247 visitors bought a ticket for the Slingshot and 237 visitors bought a ticket for the Scream Flyer. What is the probability that a randomly selected visitor bought tickets for both the Slingshot and the Scream Flyer

Answer 1

Answer:
`(204)/(1279)`

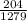
Explanation:

Formula for intersection:

n(A and B) = n(A)+n(B)-n(A or B)

Given: n(Slingshot) = 247

n(Scream Flyer)= 237

n(Slingshot or the Scream Flyer) = 280

n (Slingshot and Scream Flyer)= 247+237-280

=204

Probability of any event =
`\frac{\text{Number of favourable outcomes}}{\text{total outcomes}}`

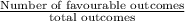
P(both the Slingshot and the Scream Flyer)=
`(204)/(1279)`

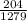
Required probability =
`(204)/(1279)`