Question

The distance from the earth to the moon is 3.84 x 105 km

a) Find this distance in metres.
b) How long would it take a spaceship to travel to the moon from earth if its average speed was 400 ms l?​

Answer 1

Part (a)

Answer:
`3.84 * 10^8 \text{ meters}`

---------------------

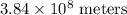
Step-by-step explanation:

Multiply by 1000 to go from km to meters.

This is because 1000 m = 1 km.

Multiplying by 1000 in scientific notation means we add 3 to the exponent 5. The 3 is because 1000 = 10^3.

So the
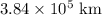`3.84 * 10^5 \text{ km}` becomes
`3.84 * 10^8 \text{ meters}`

===========================================================

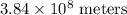
Part (b)

Answer in standard form: 960,000 seconds

Answer in scientific notation:
`9.6*10^(5) \text{ seconds}`

---------------------

Work Shown:

`\text{distance} = \text{rate}*\text{time}\\\\\text{time} = \frac{\text{distance}}{\text{time}}\\\\\text{time} = \frac{3.84 * 10^8 \text{ meters}}{400 \ \text{ m}/\text{s}}\\\\\text{time} = (3.84 * 10^8)/(4 * 10^2) \text{ seconds}\\\\\text{time} = (3.84)/(4)*(10^(8))/(10^2) \text{ seconds}\\\\\text{time} = 0.96 * 10^(8-2) \text{ seconds}\\\\\text{time} = 0.96* 10^(6) \text{ seconds}\\\\`

`\text{time} = (9.6*10^(-1))*10^(6) \text{ seconds}\\\\\text{time} = 9.6*(10^(-1)*10^(6)) \text{ seconds}\\\\\text{time} = 9.6*10^(-1+6) \text{ seconds}\\\\\text{time} = 9.6*10^(5) \text{ seconds}\\\\\text{time} = 960,000 \text{ seconds}\\\\`

To go from the scientific notation to standard form, move the decimal point 5 spaces to the right. The 5 is from the exponent.