Question

AABC - DEF. What sequence of transformations will move A ABC onto A DEF? 10 8 A(0.4) B(0,0) C(3.0) -10 -8 -6 -4:1-2 6 8 10 -2D(0.2) 24 8 -10 E(0.-10) F( 6-10)​

Answer 1

Option B

Explanation:

It's clear from the graph attached,

ΔABC has been dilated and shifted downwards.

Length of segment AB = 2 units

Length of segment DE = 4 units

Scale factor by which the dilation has been done =
`\frac{\text{Dimension of the image triangle}}{\text{Dimension of the original triangle}}`

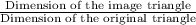
Scale factor =
`(DE)/(AB)`

=
`(4)/(2)`

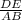
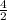
= 2

Therefore, triangle ABC is dilated by a scale factor of 2 about the origin.

Lets consider a point B(0, 0) from the given graph and analyze the transformations done.

If a point B(0, 0) is shifted to point E(0, -10) which follows the rule,

B(0, 0) → E(0 + h, 0 + k)

Here, 'h' and 'k' are the translations of the given point over x-axis and y-axis.

Therefore, (0 + h) = 0 ⇒ h = 0

0 + k = -10

k = -10

Hence, triangle ABC has been dilated by a scale factor of 2 centered at origin and followed by the translation (x, y - 10)

Option B is the correct option.