Question

Find an equation for the perpendicular bisector of the line segment whose endpoints

(5, -3) and (-7, -7).
are

Answer 1

`y=-3x-8`

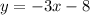
Explanation:

Hi there!

What we need to know:

• Midpoint:
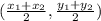  `((x_1+x_2)/(2) ,(y_1+y_2)/(2) )` where the endpoints are
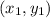  `(x_1,y_1)` and
  `(x_2,y_2)`

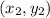
• Linear equations are typically organized in slope-intercept form:
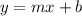  `y=mx+b` where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
• Perpendicular lines always have slopes that are negative reciprocals (ex. 2 and -1/2, 3/4 and -4/3, etc.)

1) Determine the midpoint of the line segment

When two lines bisect each other, they intersect at the middle of each line, or the midpoint.

`((x_1+x_2)/(2) ,(y_1+y_2)/(2) )`

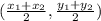
Plug in the endpoints (5, -3) and (-7, -7)

`((5+(-7))/(2) ,(-3+(-7))/(2) )\\((-2)/(2) ,(-10)/(2) )\\(-1,-5)`

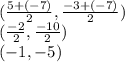
Therefore, the midpoint of the line segment is (-1,-5).

2) Determine the slope of the line segment

Recall that the slopes of perpendicular lines are negative reciprocals. Doing this will help us determine the slope of the perpendicular bisector.

Slope =
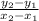`(y_2-y_1)/(x_2-x_1)` where the given points are
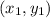`(x_1,y_1)` and
`(x_2,y_2)`

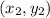
Plug in the endpoints (5, -3) and (-7, -7)

`(-7-(-3))/(-7-5)\\(-7+3)/(-7-5)\\(-4)/(-12)\\(1)/(3)`

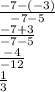
Therefore, the slope of the line segment is
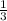`(1)/(3)`. The negative reciprocal of
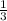`(1)/(3)` is -3, so the slope of the perpendicular is -3. Plug this into
`y=mx+b`:

`y=-3x+b`

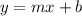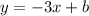
3) Determine the y-intercept of the perpendicular bisector (b)

`y=-3x+b`

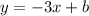
Recall that the midpoint of the line segment is is (-1,-5), and that the perpendicular bisector passes through this point. Plug this point into
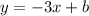`y=-3x+b` and solve for b:

`-5=-3(-1)+b\\-5=3+b`

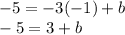
Subtract 3 from both sides

`-5-3=3+b-3\\-8=b`

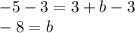
Therefore, the y-intercept of the line is -8. Plug this back into
`y=-3x+b`:

`y=-3x-8`

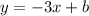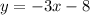
I hope this helps!