Question

how would you solve it's for algebra 2B I'm just a little stuck thanks so much for your help hope it's not a waste of time

Answer 1

Answer:
`(2x^2+s^2)/(x(x+s))`

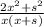
This is the fraction of 2x^2+s^2 all over x(x+s)

==============================================

Step-by-step explanation:

Currently the denominators are not the same, so we cannot subtract the fractions just yet.

We need to get the denominators equal to the LCD (lowest common denominator).

In this case, the LCD is x(x+s). Often the LCD is the product of the denominators, but not always.

To get the first fraction to have the LCD, we multiply top and bottom by x.

`(3x)/(x+s) = (x*3x)/(x(x+s)) = (3x^2)/(x(x+s))`

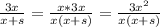
To get the second fraction to have the LCD, we multiply top and bottom by x+s

`(x-s)/(x) = ((x+s)(x-s))/(x(x+s)) = (x^2-s^2)/(x(x+s))`

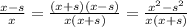
I used the difference of squares rule to go from (x+s)(x-s) to x^2-s^2.

-----------------------------------------

At this point, we have x(x+s) in both denominators and we can subtract

`(3x)/(x+s) - (x-s)/(x)\\\\(3x^2)/(x(x+s)) - (x^2-s^2)/(x(x+s))\\\\(3x^2-(x^2-s^2))/(x(x+s))\\\\(3x^2-x^2+s^2)/(x(x+s))\\\\(2x^2+s^2)/(x(x+s))\\\\`

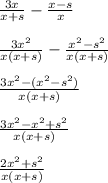
Optionally, you can distribute the x through in the denominator, but I'll leave it factored.