Question

D.sqrt(2+x^/2)
Solve this question please

Answer 1

Option a.

Explanation:

By looking at the options, we can assume that the function y(x) is something like:

`y = √(4 + a*x^2)`

`y' = (1/2)*(1)/(√(4 + a*x^2) )*(2*a*x) = (a*x)/(√(4 + a*x^2) )`

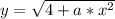
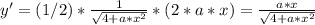
such that, y(0) = √4 = 2, as expected.

Now, we want to have:

`y' = (x*y)/(2 + x^2)`

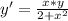
replacing y' and y we get:

`(a*x)/(√(4 + a*x^2) ) = (x*√(4 + a*x^2) )/(2 + x^2)`

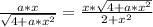
Now we can try to solve this for "a".

`(a*x)/(√(4 + a*x^2) ) = (x*√(4 + a*x^2) )/(2 + x^2)`

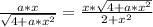
If we multiply both sides by y(x), we get:

`(a*x)/(√(4 + a*x^2) )*√(4 + a*x^2) = (x*√(4 + a*x^2) )/(2 + x^2)*√(4 + a*x^2)`

`a*x = (x*(4 + a*x^2))/(2 + x^2)`

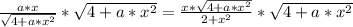
We can remove the x factor in both numerators if we divide both sides by x, so we get:

`a = (4 + a*x^2)/(2 + x^2)`

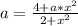
Now we just need to isolate "a"

`a*(2 + x^2) = 4 + a*x^2`

`2*a + a*x^2 = 4 + a*x^2`

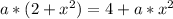
Now we can subtract a*x^2 in both sides to get:

`2*a = 4\\a = 4/2 = 2`

Then the solution is:

`y = √(4 + 2*x^2)`

The correct option is option a.