Question

Which choice is equivalent to the expression below when y2 0?
√y^2 + √16y^3 – 4y√y

Answer 1

C:YsqrtY

Explanation:

A P E X:L E A R N I N G

Answer 2

Option C.

Explanation:

We start with the expression:

`√(y^3) + √(16*y^3) - 4*y√(y)`

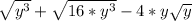
where y > 0. (this allow us to have y inside a square root, so we don't mess with complex numbers)

We want to find the equivalent expression to this one.

Here, we can do the next two simplifications:

`√(16*y^3) = √(16) √(y^3) = 4*√(y^3)`

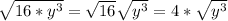
And:

`y*√(y) = √(y^2) *√(y) = √(y^2*y) = √(y^3)`

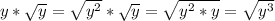
If we apply these two to our initial expression, we can rewrite it as:

`√(y^3) + √(16*y^3) - 4*y√(y)`

`√(y^3) + 4*√(y^3) - 4√(y^3) = √(y^3)`

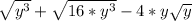
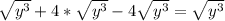
Here we can use the second simplification again, to rewrite:

`√(y^3) = y*√(y)`

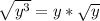
So, concluding, we have:

`√(y^3) + √(16*y^3) - 4*y√(y) = y*√(y)`

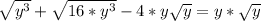
Then the correct option is C.