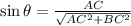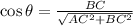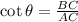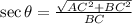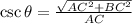Question

Given the following trigonometric ratio, enumerate the meaning ratio ​

Answer 1

The trigonometric ratios are presented below:

`\sin \theta = \frac{AC}{\sqrt{AC^(2) + BC^(2)}}`

`\cos \theta = \frac{BC}{\sqrt{AC^(2) + BC^(2)}}`

`\cot \theta = (BC)/(AC)`

`\sec \theta = \frac{\sqrt{AC^(2)+BC^(2)}}{BC}`

`\csc \theta = \frac{\sqrt{AC^(2)+BC^(2)}}{AC}`

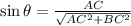
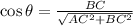
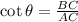
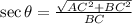
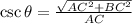
Explanation:

From Trigonometry we know the following definitions for each trigonometric ratio:

Sine

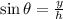`\sin \theta = (y)/(h)` (1)

Cosine

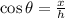`\cos \theta = (x)/(h)` (2)

Tangent

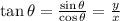`\tan \theta = (\sin \theta)/(\cos \theta) = (y)/(x)` (3)

Cotangent

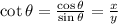`\cot \theta = (\cos \theta)/(\sin \theta) = (x)/(y)` (4)

Secant

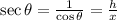`\sec \theta = (1)/(\cos \theta) = (h)/(x)` (5)

Cosecant

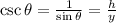`\csc \theta = (1)/(\sin \theta) = (h)/(y)` (6)

Where:

`x` - Adjacent leg.

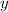`y` - Opposite leg.

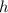`h` - Hypotenuse.

The length of the hypotenuse is determined by the Pythagorean Theorem:

`h = \sqrt{x^(2)+y^(2)}`

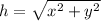
If
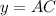`y = AC` and
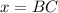`x = BC`, then the trigonometric ratios are presented below:

`\sin \theta = \frac{AC}{\sqrt{AC^(2) + BC^(2)}}`

`\cos \theta = \frac{BC}{\sqrt{AC^(2) + BC^(2)}}`

`\cot \theta = (BC)/(AC)`

`\sec \theta = \frac{\sqrt{AC^(2)+BC^(2)}}{BC}`

`\csc \theta = \frac{\sqrt{AC^(2)+BC^(2)}}{AC}`