Answer:
Remember that:
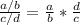
A) We know that:
Each dog gets (2/3) of a cup of food.
Elena used 3 + 1/3 cups of dog food, then, how many dogs there are?
The number of dogs is equal to the quotient between the total amount of food used and the food that a single dog needs, this is:
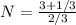
We can rewrite the numerator as:
3 + 1/3 = 3*(3/3) + 1/3 = 9/3 + 1/3 = 10/3
Replacing that in the above equation, we get:
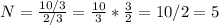
There are 5 dogs.
B)
We know that:
5 + 1/8 cups of water, can fill four bottles.
Then, how many cups we need for each bottle?
Assuming that each bottle holds the same amount of water, then each bottle will hold a fourth of (5 + 1/8) cups of water.
This is the quotient between (5 + 1/8) cups of water and 4.
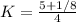
We can rewrite the numerator as:
5 + 1/8 = 5*(8/8) + 1/8 = 40/8 + 1/8 = 41/8
Replacing that we get:
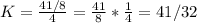
We can rewrite this as a mixed number in the next way:
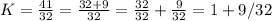
So with 1 and 9/32 cups of water we can fill one of the bottles.