Answer:
The answer is "triangle ABC is not a right triangle".
Explanation:
For a right-angle triangle:
Its square upon on longest or triangular edges is equivalent to the total of the other two squares
Its parameters indicated throughout the question are;
Square of lateral length
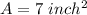
The square of lateral length
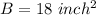
The square of lateral length
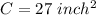
Thus, the longest side is C, as well as the size
 of the squares of its two sides, is
of the squares of its two sides, is
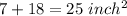 , lower than square
, lower than square
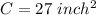 , hence, the ABC triangle is not correct. Its longest edge is consequently C.
, hence, the ABC triangle is not correct. Its longest edge is consequently C.