Answer:
a) z-distribution is used, as we have the standard deviation for the population.
b) Between
 and
and
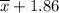 , in which
, in which
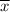 is the sample mean of tics per hour.
is the sample mean of tics per hour.
Explanation:
a. To compute the confidence interval use a, z or t distribution?
We have the standard deviation for the population, and thus, the z-distribution is used.
b. With 90% confidence the population mean number of tics per hour that children with Tourette syndrome exhibit is between ______ and _______ .
We have that to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
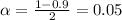
Now, we have to find z in the Z-table as such z has a p-value of
 .
.
That is z with a pvalue of
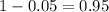 , so Z = 1.645.
, so Z = 1.645.
Now, find the margin of error M as such

In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
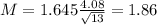
The lower end of the interval is the sample mean subtracted by M. So it is

The upper end of the interval is the sample mean added to M. So it is
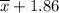
Between
 and
and
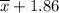 , in which
, in which
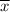 is the sample mean of tics per hour.
is the sample mean of tics per hour.