Question

If 2 is added to the numerator of a

fraction it reduces to 1/2 and if 1 is subtracted from the denominater it reduces to 1/3. Find the fraction.​

Answer 1

❍ Let's say, that the numerator of the fraction be x and denominator of the fraction be y.

⠀⠀⠀⠀⠀━━━━━━━━━━━━━━━━━━━⠀⠀⠀⠀⠀⠀⠀⠀

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\underline{\sf{Case\;}\it{1}:}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

• If 2 is added to the numerator of the fraction, it reduces to 1/2.

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

Therefore,

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\begin{gathered}:\implies\sf{(x+2)/(y)=(1)/(2)}\\\\\\:\implies\sf{2x+4=y}\\\\\\:\implies\sf{2x=y-4}\qquad\qquad\bigg\lgroup\sf{eq^n\;1}\bigg\rgroup\end{gathered}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\underline{\sf{Case\;}\it{2}:}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

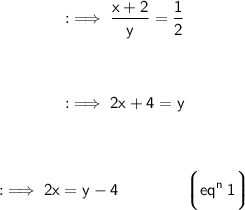
• If 1 is subtracted from the denominator of the fraction, it reduces to 1/3.

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

Therefore,

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\begin{gathered}:\implies\sf{(x)/(y-1)=(1)/(3)}\\\\\\:\implies\sf{3x=y-1}\qquad\qquad\bigg\lgroup\sf{eq^n\;2}\bigg\rgroup\end{gathered}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\qquad\qquad\footnotesize{\underline{\bf{\dag\;}\frak{Subtracting\;eq^n\;2\;from\;eq^n\;1:}}}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\begin{gathered}:\implies\sf{3x-2x=y-1-y-4}\\\\\\:\implies\underline{\boxed{\pink{\frak{\pmb{x=3}}}}}\;\bigstar\end{gathered}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\qquad\qquad\footnotesize{\underline{\bf{\dag\;}\frak{Substituting\;value\;of\;x\;in\;eq^n\;1:}}}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\begin{gathered}:\implies\sf{2x=y-4}\\\\\\:\implies\sf{2(3)=y-4}\\\\\\:\implies\sf{6=y-4}\\\\\\:\implies\sf{6=y-4}\\\\\\:\implies\sf{y=-4-6}\\\\\\:\implies\underline{\boxed{\purple{\frak{\pmb{y=10}}}}}\;\bigstar\end{gathered}`

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

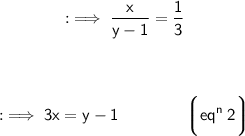
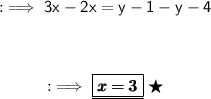
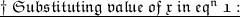
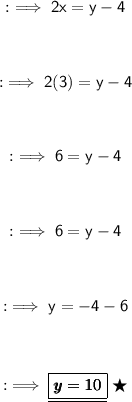
Hence,

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

• Numerator = x = 3
• Denominator = y = 10

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

`\therefore\;{\underline{\sf{Hence,\;the\;fraction\;is\;\frak{(3)/(10)}}.}}`⠀⠀