The correct option is A:
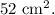
To find the surface area of the given solid step by step, we consider all the visible faces:
1. Calculate the area of the base rectangle (on the bottom):
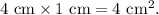
2. Calculate the area of the front rectangle:
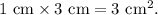
3. Calculate the area of the back rectangle (on the top):
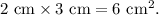
4. Calculate the area of the left-side rectangle:
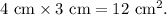
5. Calculate the area of the right-side rectangle (this is the vertical side on the far right):
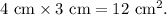
6. Calculate the area of the top surface (this includes two parts: the 1 cm wide strip and the 2 cm wide strip, both 4 cm long):
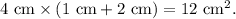
Now, add all these areas together to get the total surface area:
![\[ 4 + 3 + 6 + 12 + 12 + 12 = 49 \text{ cm}^2 \]](https://img.qammunity.org/2022/formulas/mathematics/college/mynw47qj36mlc8efxqlkpyj9cpkka1e18n.png)
However, since this result is not one of the options provided, we should check our calculations for any possible oversight or missing faces.
Upon re-evaluating the image, it is clear that we should also consider the small vertical face on the left that measures
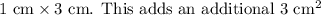 to the total surface area.
to the total surface area.
So, the correct total surface area of the solid is:
![\[ 49 \text{ cm}^2 + 3 \text{ cm}^2 = 52 \text{ cm}^2 \]](https://img.qammunity.org/2022/formulas/mathematics/college/ibiodyeb32izqyvjxlq0urs9e5p0k1xpq1.png)