The integral that represent the area enclosed by y = x +1, y = 4-X y = 0,X = 0 is:

Question

asked Mar 23, 2022 104k views

1 Answer

Tobias Geiselmann · Answer 1 · 2022-03-27T07:58:09+0000

Answer:

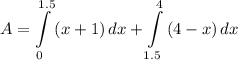
$\displaystyle A = \int\limits^(1.5)_0 {(x + 1)} \, dx + \int\limits^4_(1.5) {(4 - x)} \, dx$

General Formulas and Concepts:

Algebra I

Calculus

Integrals - Area under the curve

Explanation:

Step 1: Define

Identify

y = x + 1

y = 4 - x

y = 0

x = 0

Step 2: Identify Info

Graph the functions - See Attachment

Bounds of Integration: [0, 4]

Point of Intersection: x = 1.5

Step 3: Find Area

Set up [Integral - Area]:
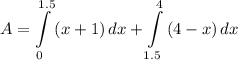
$\displaystyle A = \int\limits^(1.5)_0 {(x + 1)} \, dx + \int\limits^4_(1.5) {(4 - x)} \, dx$

Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Integration - Area under the curve

Book: College Calculus 10e