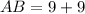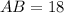Question

Chord \displaystyle \overline{AB} AB is 12 inches from center \displaystyle OO. If the radius has a length of \displaystyle 1515 inches, find the length of chord \displaystyle \overline{AB} AB .

Answer 1

18 inches

Explanation:

Given

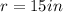`r = 15in` --- radius

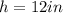`h = 12in` --- distance between chord and the center of the circle

Required

The chord length

See attachment for illustration

First, calculate distance AX using Pythagoras theorem.

`AO^2 = AX^2 + OX^2`

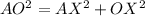
This gives:

`15^2 = AX^2 + 12^2`

`225 = AX^2 + 144`

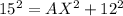
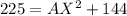
Collect like terms

`AX^2 = 225 - 144`

`AX^2 = 81`

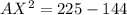
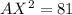
Take square roots of both sides

`AX = 9`

AB is then calculated as:

`AB= AX + XB`

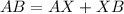
Where:

`AX=XB =9`

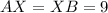
So:

`AB = 9 + 9`

`AB = 18`