Question

What is an equation of the line that passes through the point (8, 2) and is parallel to the line 5x - 4y = 36?​

Answer 1

`y=(5)/(4)x-8`

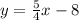
Explanation:

Hi there!

What we need to know:

• Linear equations are typically organized in slope-intercept form:
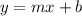  `y=mx+b` where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
• Parallel lines always have the same slopes and different y-intercepts

1) Determine the slope (m)

`5x - 4y = 36`

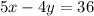
Rearrange the given equation into y-intercept form (this will help us determine m)

Subtract 5x from both sides

`5x - 4y-5x = -5x+36\\-4y=-5x+36`

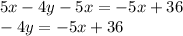
Divide both sides by -4

`y=(5)/(4) x-9`

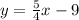
Now, we can see that
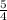`(5)/(4)` is in the place of m, making it the slope. Because parallel lines have the same slopes, the slope of the line we're solving for is therefore
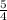`(5)/(4)`. Plug this into
`y=mx+b`:

`y=(5)/(4)x+b`

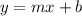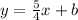
2) Determine the y-intercept (b)

`y=(5)/(4)x+b`

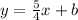
Plug in the given point (8,2) and solve for b

`2=10+b`

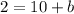
Subtract 10 from both sides

`2-10=10+b-10\\-8=b`

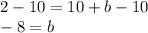
Therefore, the y-intercept is -8. Plug this back into
`y=(5)/(4)x+b`:

`y=(5)/(4)x-8`

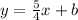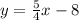
I hope this helps!