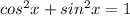Question

Prove each of these identities.

(a) tan x + cot x = secx cosecx
(b) cosec x - sin x = cos x cot x​

Answer 1

Identity (a) can be re-written as

`sec x\ cosec x - cot x = tan x`

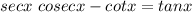
which we already proven in another question, while for idenity (b)

`(A)\frac 1 {sin x} -sin x = cos x (cos x)/(sin x)\\\\(B)\frac {1-sin^2x}{sin x} = \frac {cos^2x} {sin x} \\\\(C) \frac {cos^2x}{sin x} =\frac {cos^2x} {sin x}`

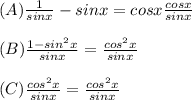
step A is simply expressing each function in terms of sine and cosine.

step B is adding the terms on the LHS while multiplying the one on RHS.

step C is replacing the term on the numerator with the equivalent from the pithagorean identity
`cos^2x + sin^2x = 1`