Answer:
Step-by-step explanation:
This is quite tricky! You need to do 2 different equations to solve all the parts of this problem. First is finding the acceleration in one dimension, which has an equation of
F - f = ma
where F is the applied Friction,
f is the frictional force acting against F,
m is the mass of the object, and
a is the acceleration of the object (NOT the velocity!)
This is Newton's Second Law expanded on a bit. The sum of the forces working on an object is equal to the object's mass times its acceleration. We have F, but we need f which is found in the equation
f = μ
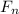 which is the coefficient of kinetic friction times the weight of the object. Weight is found in the equation
which is the coefficient of kinetic friction times the weight of the object. Weight is found in the equation
w = mg where m is mass and g is the pull of gravity. Let's start there and work backwards:
w = 37(9.8) to 2 sig figs so
w = 360N. Now fill that in to find f:
f = (.17)(360) to 2 sig figs so
f = 61. Now for the final answer in the original equation way back up at the top:
85 - 61 = 37a and do the subtraction on the left side first:
24 = 37a and then we divide to 2 sig figs to get
a = .65 m/s/s
Since we are moving in a straight line (as opposed to on an angle) the displacement is found in
d = rt which simply says that the distance an object moves is equal to its rate times the time. Therefore,
d = 2.2(3.4) to 2 sig figs so
d = 7.5 m