2 Answers

Andy MacKinlay · Answer 1 · 2022-05-24T08:03:55+0000

Name of the polygon: Trapezoid

Length of line segment AD: 5 units

Area of the trapezoid: 20 square units.

The points A (-2, 2), B (-4, -4), C (1, -4), and D (3, 2) form a trapezoid. To find the name of the polygon, we need to look at its properties.

Number of sides: The polygon has 4 sides.

Parallelogram properties: The opposite sides are not parallel, so it is not a parallelogram.

One pair of parallel sides: Sides AD and BC are parallel.

Therefore, the polygon is a trapezoid.

The length of line segment AD. We can use the distance formula:

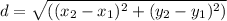
$d = \sqrt{((x_2 - x_1)^2 + (y_2 - y_1)^2)$

where
(x_1, y_1) are the coordinates of point A and
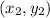(x_2, y_2) are the coordinates of point D. Plugging in the values, we get:

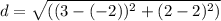
$d =\sqrt{((3 - (-2))^2 + (2 - 2)^2)$

$d = \sqrt{((5)^2 + (0)^2)$

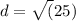
$d = \sqrt(25)$

d = 5

Therefore, the length of line segment AD is 5 units.

Find the area of the trapezoid. We can use the formula:

Area = 1/2 * (base1 + base2) * height

where:

base1 is the length of side AD (5 units)

base2 is the length of side BC (we need to find this)

height is the distance between the parallel sides (4 units)

We can find the length of base BC using the distance formula again between points B and C:

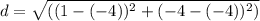
$d = \sqrt{((1 - (-4))^2 + (-4 - (-4))^2)$

$d = \sqrt{((5)^2 + (0)^2)$

d = 5

Therefore, base2 is also 5 units. Plugging all the values into the area formula, we get:

Area = 1/2 * (5 + 5) * 4

Area = 1/2 * 10 * 4

Area = 20

Therefore, the area of the trapezoid is 20 square units.

Please log in or register to add a comment.