Correct Questions :-
Find the values of P for which the quadratic equation 4x²+px+3=0 , provided that roots are equal or discriminant is zero .
Solution:-
Let us Consider a quadratic equation αx² + βx + c = 0, then nature of roots of quadratic equation depends upon Discriminant (D) of the quadratic equation.
For equal roots
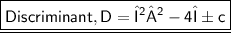
So,
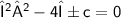
Here,
Now,
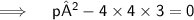
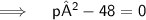
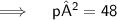
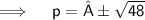
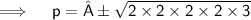
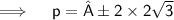
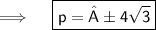
Thus, the values of P for which the quadratic equation 4x²+px+3=0 are-
4√3 and -4√3.